Cours Mathématiques - Théorème de Thalès et sa réciproque 1ère Année Secondaire

Cours Mathématiques - Théorème de Thalès et sa réciproque  1ère Année Secondaire

Théorème de Thalès : Soient (BM) et (CN) deux droites sécantes en A. Si les droites (BC) et (MN) sont parallèles, alors :

AMAB=ANAC=MNBC

Réciproque du théorème de Thalès : Soient (BM) et (CN) deux droites sécantes en A. 

Si : 

• 

AMAB=ANAC$\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$ 

• les points A, M, B et les points A, N, C sont alignés dans le même ordre. 

Alors :

les droites (MN) et (BC) sont parallèles. 

Exemple :

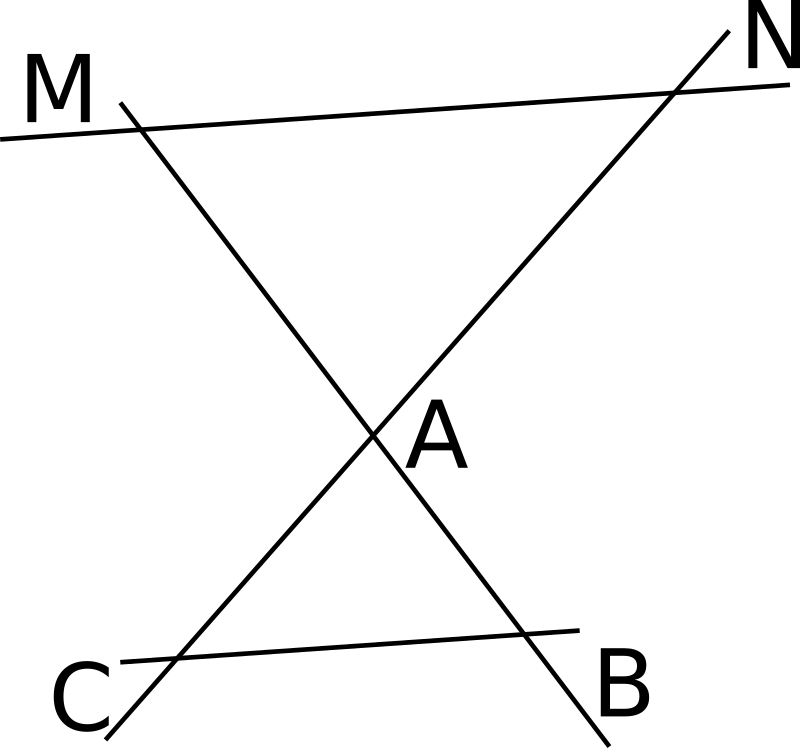
On sait que :

• les droites (BM) et (CN) sont sécantes en A.

• 

AMAB=ANAC$\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$

• Les points M, A, B et N, A, C sont alignés dans cet ordre.

Conséquence du théorème de Thalès

- ABC et AMN sont deux triangles ;
- M ∈ (AB) ;
- N ∈ (AC).

Si , alors les droites (BC) et (MN) ne sont pas parallèles.